Output Adaptive Simulation: Is it Machine Learning?

Oh, short answer, "yes" with an "if." Long answer, "no" with a "but."

-- Reverend Lovejoy, "Hurricane Neddy"

When I explain my research to friends and family, they often ask me whether output adaptivity is some kind of machine learning. Initially, I was fairly certain that output adaptivity was not machine learning. However, the more I thought about it, the less certain I became. Now I think it may be fair to describe output adaptivity as a kind of machine learning for the grid generation process. I’m not an expert on machine learning, so I’ll try to stay away from strong claims, but I decided to lay out my thoughts anyway.

Lets start by defining what machine learning is. Steven Knox describes learning in the following way^[1]:

The Problem of Learning. There are a known set $\mathcal{X}$ and an unknown function $f$ on $\mathcal{X}$. Given data, construct a good approximation $\hat{f}$ of $f$. This is called learning $f$.

So, I think its fair to say that if we’re using an automated process to learn $f$, then we’re machine learning. With this definition in hand, lets see if there are any parallels between machine learning and output adaptive simulation.

For a given physical domain, we can think of there being a set of all possible valid grids we could construct within that domain. On each of those grids, we could calculate a solution to the governing equations, and from there calculate an output of interest (e.g. drag) with an associated discretization error. The purpose of output adaptive simulation is to find the grid (from the set of valid grids), which minimizes the discretization error. Referring back to Knox’s definition, we can define $\mathcal{X}$ as the set of possible grids, and $f$ is the discretization error in the specified output.

This is starting to sound like machine learning; we’re trying to optimize against a function which doesn’t have a closed form. But are we using machine learning to do it? That depends if we construct an approximation to $f$ using data as part of the optimization process.

In Professor David Darmofal’s research group, we use an output adaptive algorithm called Mesh Optimization via Error Sampling and Synthesis (MOESS)^[2].

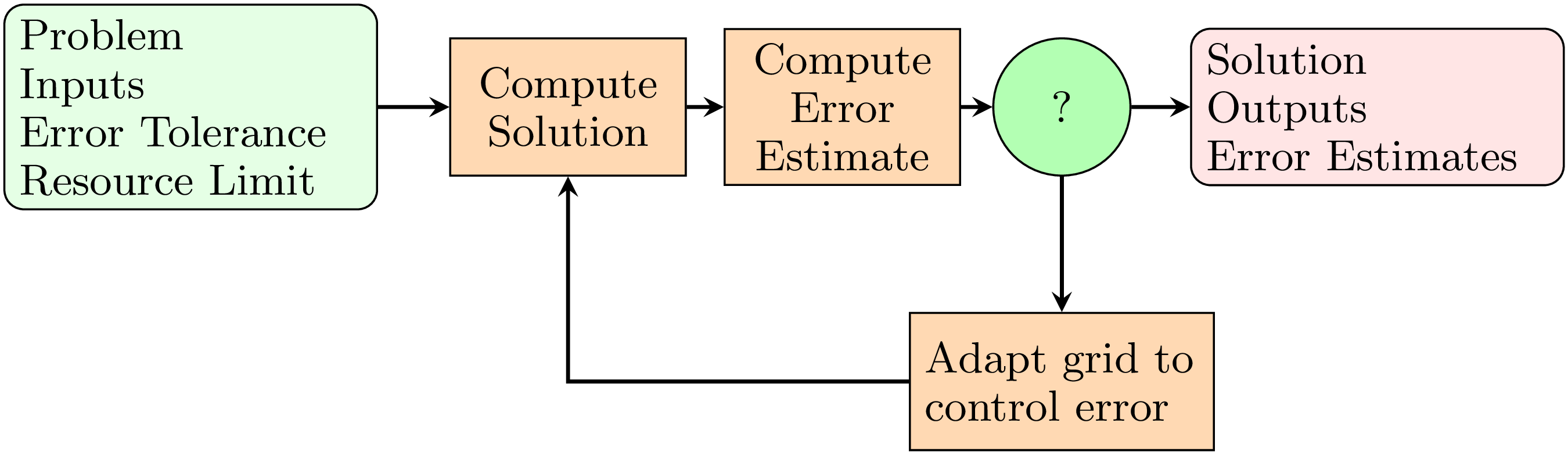
The MOESS-magic happens in the box labeled "Adapt grid to control error". In this step we estimate the change in discretization error when locally refining the grid, and then use this data to construct a surrogate model of the error with respect to the grid. It is this surrogate model which we optimize against.

The construction of the surrogate model is what makes MOESS machine learning. We take training data (in the form of local refinements of a grid), learn the function between the grid and the discretization error (i.e. the surrogate model is $\hat{f}$), and then optimize against it. To me, at least, this sounds like using machine learning to generate optimal grids.

I have to admit, when I hear "machine learning for grid generation", I still think of something like taking a large number of hand generated grids over a range of problems and "machine learning" those, maybe with some kind of deep neural net. Output adaptive simulation is very different from that -- iteratively testing and modifying grids until an optimal grid is found. I'm not sure if the impression I have indicates that I am missing something in how I am assessing output adaption as machine learning. Does machine learning require big data? What about a priori models? Maybe my impressions of machine learning are based on marketing more than engineering.

What do you think? Am I missing something in how I’m looking at machine learning? Is the connection obvious? Reach out to me on LinkedIn or Twitter and let me know!