My research is on robust output adaptive simulation. As computational fluid dynamics (CFD) becomes an important part of the aerospace design process, the correctness of simulation results is becoming increasingly important. Output adaptive simulation is a tool to increase the quality of CFD results, while reducing effort expended by the engineer. Thus, it increases the confidence in results from CFD, while reducing their cost
What is Output Adaptive Simulation?
Typically, engineers are interested in obtaining estimates of output quantities (e.g. lift or drag) from CFD simulations. The differences between simulated results and real-world performance can come from several sources, including,
- Modeling errors – the physics being modeling is insufficient or incorrect.
- Aleatory and epistemic uncertainties – natural randomness in the process, and uncertainty in the inputs or key parameters.
- Discretization errors – solving the governing equations in an approximate sense on a discrete grid rather than analytically.
Output adaptive simulation is a method for optimizing the computational grid used in a simulation to minimize the error due to discretization in a specified output quantity at a given computational cost. Output adaptive methods also generate an estimate for the error in the output due to the discretization, allowing engineers to quantify the accuracy of their CFD data.
Aren’t “best practices” and uniform refinement sufficient?
In general, no (although I might be biased). For example, we can look at the results from the 3rd AIAA Drag Prediction Workshop[1]. The coefficient of drag as a function of grid size is shown for a wing-only configuration below[2]. This data was obtained by two different groups using the same CFD code, with the same turbulence model. However, the CFD code was run on grids that were independently generated using “best practices” from each group, and then uniformly refining from these initial grids.
We can see, as Mavriplis[1:1] notes,
… the two families of grids do not appear to be converging to the same continuum values in the limit of infinite mesh resolution.
The two different sets of best practices predict significantly different estimates of the drag. Clearly, without an estimate of the error, it is not clear which set of results is providing the most accurate estimate of drag at each grid size.
How does it work?
The output adaptive algorithm we use in my research group is an iterative process, outlined in the diagram below.
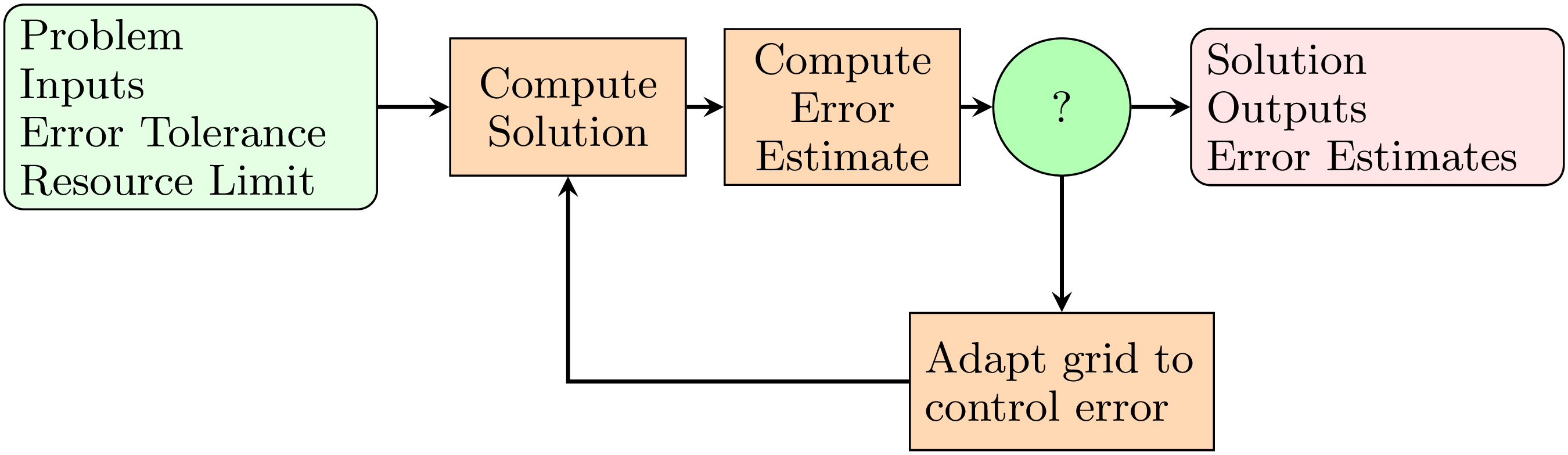
The solution is found on an initial grid. Using this solution, we can find the error that each element contributes to the total error in a user specified output quantity. These local estimates are then used to generate a surrogate model for how the error varies with the grid. This surrogate model is then used optimize the grid to minimize error. We then find this solution on the new grid, and repeat this process until we have met a termination criterion (e.g. an error tolerance).
Where does my research fit in?
My research focuses on being able to compute the solution on any valid grid the algorithm could generate. This broadly falls into two parts,
- Stabilization operators
- Algorithms to solve nonlinear problems
The first part is concerned with the existence of a discrete solution, and if it is physical (think positive density and temperature). Whereas, the second part is concerned with finding this solution, given it exists.
Can this be applied to non-aerospace problems?
Yes, this method can be applied to (almost) any non-chaotic problem that can be written as,
$$\frac{\partial u}{\partial t} + \nabla\cdot\left[\vec{F}\left(u\right) - \kappa\left(u\right)\nabla u\right] + S\left(u, \grad u\right) - f\left(\vec{x}\right) = 0.$$
Adaptivity in the context of chaotic problems is currently being researched by a collaborator of mine, Cory Frontin.
Mavriplis, D. J., “Results from the 3rd Drag Prediction Workshop Using the NSU3D Unstructured Mesh Solver,” AIAA Paper 2007-256, 2007. https://doi.org/10.2514/6.2007-256 ↩︎ ↩︎